The Lac in FracLac stands for lacunarity.
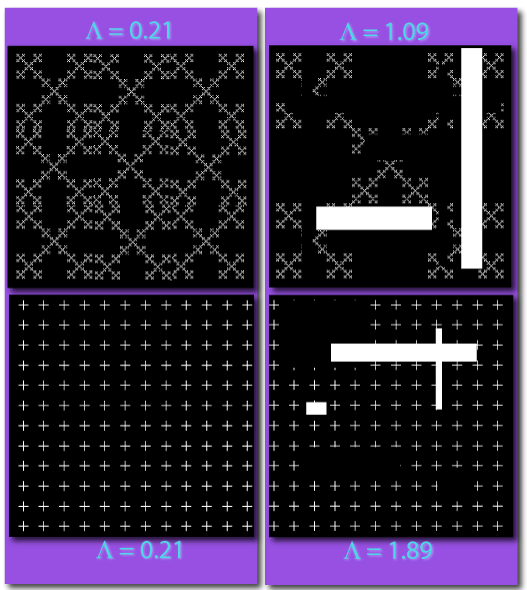
The word "lacunarity" literally refers to a gap or pool as derived from the word for "lake", but in morphological analysis it has been variously defined as gappiness, visual texture, inhomogeneity, translational and rotational invariance, etc. Usually denoted as Λ or λ, in FracLac, lacunarity pertains to both gaps and heterogeneity. The general concept is illustrated in the images shown below, which increase in lacunarity from left to right. To see how this relates to their invariance and gappiness, hover your mouse back and forth over the images to rotate them 90° and back.
Gaps and Heterogeneity or Rotational and Translational Invariance if you prefer
As you hover your mouse back and forth above, you can see that the left and centre images are both essentially unchanged when rotated 90°. They have similarly low lacunarity values, but the centre one has more gaps in it than does the left, and this is paralleled in its slightly higher lacunarity value. The rightmost figure, in contrast, changes noticeably when rotated 90° and has many more irregular gaps than either of the other two images.
Comparing two of those images to other images below further highlights differences in lacunarity calculated in FracLac. The top left figure (which was discussed above but is shown here again for comparison) is similar to the bottom left. Both have virtually the same numbers of black and white pixels and the pixels are arranged in both cases in homogeneous, somewhat translationally and rotationally invariant patterns, and both have virtually the same low lacunarity as a result. On the right, in contrast, the images show greater variation and gaps than those on the left, and have correspondingly higher lacunarities. When comparing the bottom and top on the right, however, both have irregular gaps and are no longer rotationally and translationally invariant. But it is not as obvious that the lower right figure has greater lacunarity than the upper right without reference to the objective indices.
FracLac delivers lacunarity based on variation in pixel density at different box sizes in fixed scans and sliding scans.
The values above were calculated using the pixel distribution. To find the pixel distribution, the number of pixels in each ε-sized box in a grid that was placed on an image is counted during standard nonoverlapping or overlapping box counting. Then, lacunarity or λ for each grid of calibre ε is calculated from the standard deviation, σ, and mean, μ, for pixels per box. That is, there is a λ value for each ε in each series of grid sizes in each g, grid orientation, in a set of grid orientations, as shown in the formula in the next column.
λε,g = CVε,g2=(σε,g⁄με,g)2.
- FracLac reports all of the values for λε,g
- graphs how λ∝ε.
- reports on each grid position, g, the Λg=λ (i.e., the average λ over all ε)
- gives one summarized value for an image from all orientations, the average of the average or Λ.
- and reports multiple values for local scans
The Technical Section tells more about how to interpret lacunarity with FracLac.
Catch your breath.
Whew. That was a lot of symbology and linkage for one paragraph. So, you've got gappiness and heterogeneity down, and you know about the different levels of lacunarity. The next thing you can read about on this page is how lacunarity and the fractal dimension work together, or, you might say, why Frac needs Lac.
Practical
Supplementing the
DBLacunarity and fractal dimensions work together to characterize patterns extracted from digital images.As the picture below illustrates, sometimes patterns having identical fractal dimensions will be distinguishable by their lacunarity, or vice versa.
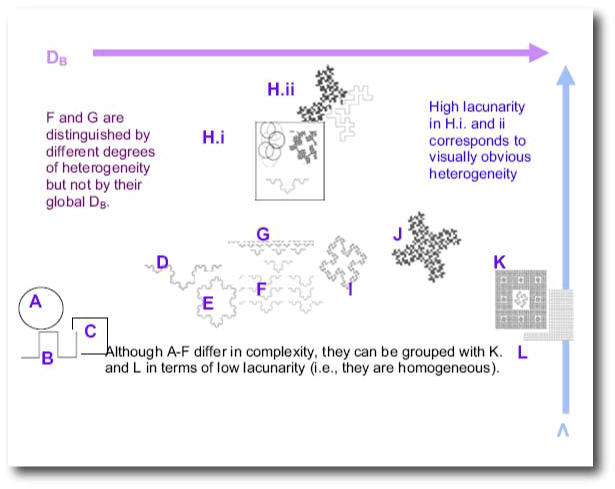
Types of Lacunarity
Now that you have finished with this page, you might want to pursue some ideas rather than go on with the normal flow using the arrows. If you do go on in that way, you will find in the next section, on multifractals, that lacunarity and multifractal analyses also go together very nicely to describe complex forms. If you want to divert yourself and build more on this page, find out some details about the actual results you might get when using FracLac, go here or check out the list below of some hand-picked examples of types of lacunarity in FL from the glossary - I must admit, though, that these are full of formulae and just might tax your brain if you read them all at once:
