
Is your cell roundish or off-centre?
Is it oblong? Is it spiky? Are you hoping, when trying to describe a particularly indescribable cell or structure you saw under the scope, to include measures that might supplement complexity? In addition to fractal and lacunarity data, FracLac returns other measures that help describe the indescribable. The information returned helps define the 2-dimensional space occupied by, for instance, biological structures, and offers ways to quantify features such as roundness or circularity, elongation, and irregularity ("spikiness").
FracLac returns metrics based on the convex hull, bounding circle, and bounding box of binary images.
In FracLac, the convex hull is made by finding the "outermost" foreground pixels and joining them with straight line segments as in the figure below.
The bounding circle is calculated using the maximum span across or else the three points defining the smallest circle around the convex hull.
The smallest box enclosing the foreground pixels of an image as oriented on the screen is the bounding box. This box is used to calculate scale and is reported in the standard results table.
All of the metrics together (see below) describe a boundary defining the size and shape of the two dimensional space occupied by the foreground pixels of an image.You have the option to create graphics files showing the hull and circlealong with the metrics file.
Is this Fractal Analysis?
You don't need these morphometrics to do fractal analysis per se, but you can use them to supplement your study. The parameters returned include the circle's diameter and the convex hull's area, perimeter, radii, circularity, vertical and horizontal dimensions, and span ratio, as well as the number and density of pixels.
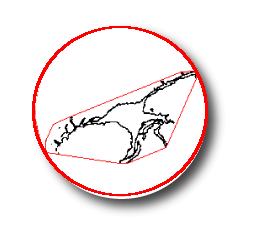
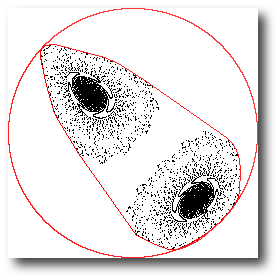 These images show the convex hull and bounding circle for a
Henon multifractal
and a neuron. FracLac draws the hull
and circle if you select
them from the
box counting,
LCFD,
or sub scan options panels.
These images show the convex hull and bounding circle for a
Henon multifractal
and a neuron. FracLac draws the hull
and circle if you select
them from the
box counting,
LCFD,
or sub scan options panels.